Multiple Choice
light on top of the car turns at a rate of revolution per second. The rate at which the light beam moves along the wall is . Find the rate when is .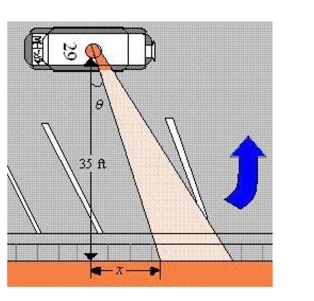
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q71: Find the value of c guaranteed
Q72: <span class="ql-formula" data-value="\text { Find the }
Q73: Find the <span class="ql-formula" data-value="x"><span
Q74: A ring has a inner circumference of
Q75: <span class="ql-formula" data-value="\text { Let } f
Q77: Determine the limit (if it exists).
Q78: Use the rectangles in the graph
Q79: <span class="ql-formula" data-value="\text { Find all vertical
Q80: Find all the vertical asymptotes (if
Q81: 25-foot ladder is leaning against a