25-Foot Ladder Is Leaning Against a House (See Figure) $r = \frac { 2 x } { \sqrt { 625 - x ^ { 2 } } } \mathrm { ft } / \mathrm { sec }$

Multiple Choice

25-foot ladder is leaning against a house (see figure) . If the base of the ladder is pulled away from the house at a rate of 2 feet per second, the top will move down the wall at a rate of $r = \frac { 2 x } { \sqrt { 625 - x ^ { 2 } } } \mathrm { ft } / \mathrm { sec }$ where $x$ is the distance between the base of the ladder and the house. Find the limit of 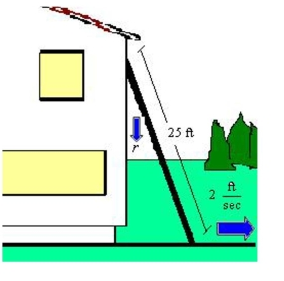$r$ as $x \rightarrow 25 ^ { - }$ .

A) $- \infty$
B) 50
C) 0
D) $\infty$
E) 25