Multiple Choice
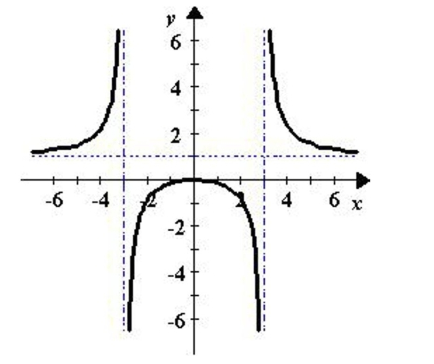
is differentiable.
A) is differentiable at .
B) is differentiable everywhere except at .
C) is differentiable everywhere except at .
D) is differentiable on the interval .
E) is differentiable on the interval .
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q34: Suppose the position function for a
Q35: Suppose the position function for a
Q36: Find the derivative of the function.
Q37: <span class="ql-formula" data-value="\text { Approximate the fixed
Q38: A ball is thrown straight down
Q40: <span class="ql-formula" data-value="\text { Find } \frac
Q41: <span class="ql-formula" data-value="\text { Use implicit differentiation
Q42: A projectile is shot upwards from
Q43: Find the rate of change of
Q44: A petrol car is parked 50