Multiple Choice
Find the eccentricity and distance from the pole to the directrix of the conic. Then sketch and identify the graph. Use a graphing utility to confirm your results.
A) eccentricity:
distance from pole to directrix: 2
The graph is an ellipse.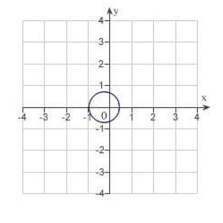
B) eccentricity: 3
distance from pole to directrix:
The graph is an ellipse.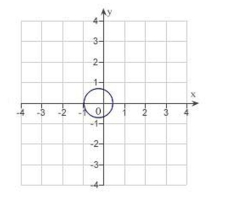
C) eccentricity:
distance from pole to directrix:
The graph is an ellipse.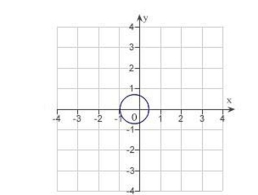
D) eccentricity: 3
distance from pole to directrix: 2
The graph is a hyperbola.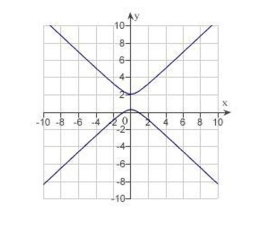
E) eccentricity: 3
distance from pole to directrix:
The graph is a hyperbola.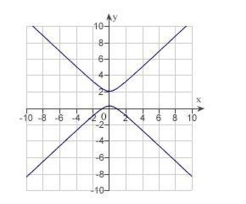
Correct Answer:

Verified
Correct Answer:
Verified
Q6: Classify the graph of the equation
Q7: Find the area of the inner
Q8: Find the directrix of the parabola
Q9: <span class="ql-formula" data-value="\text { Find } \frac
Q10: <span class="ql-formula" data-value="\text { Find the area
Q12: <span class="ql-formula" data-value="\text { Identify the conic
Q13: Find a set of parametric equations
Q14: <span class="ql-formula" data-value="\text { Identify the graph
Q15: <span class="ql-formula" data-value="\text { Identify any points
Q16: Find an equation of the tangent