Multiple Choice
Find a piecewise smooth parametrization of the path C given in the following graph. 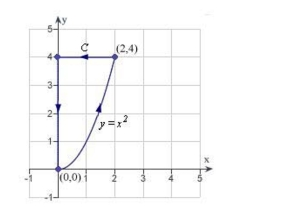
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q95: Find a piecewise smooth parametrization of
Q96: Find the rectangular equation for the
Q97: Find the divergence of the vector
Q98: Set up and evaluate a line
Q99: Use Green's Theorem to evaluate the
Q101: Find the area of the surface
Q102: Determine whether the vector field is
Q103: Let S be the oriented upwards.
Q104: Write a set of parametric equations
Q105: Find the conservative vector field for