Compare the Right-Hand and Left-Hand Derivatives to Determine Whether or Not

Multiple Choice

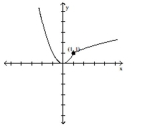
Compare the right-hand and left-hand derivatives to determine whether or not the function is differentiable at the point whose coordinates are given.
- $y=x^{2} \quad y=\sqrt{x}$

A) Since $\lim _ { x \rightarrow1 ^ { + } } \mathrm { f } ^ { \prime } ( \mathrm { x } ) = 2$ while $\lim _ { x \rightarrow 1 ^ { - } } \mathrm { f } ^ { \prime } ( \mathrm { x } ) = \frac { 1 } { 2 } , \mathrm { f } ( \mathrm { x } )$ is not differentiable at $x = 1$ .
B) Since $\lim _ { x \rightarrow 1^ { + } } \mathrm { f } ^ { \prime } ( x ) = \frac { 1 } { 2 }$ while $\lim _ { x \rightarrow 1 ^ { - } } \mathrm { f } ^ { \prime } ( \mathrm { x } ) = 1 , \mathrm { f } ( \mathrm { x } )$ is not differentiable at $x = 1$ .
C) Since $\lim _ { x \rightarrow1 ^ { + } } f ^ { \prime } ( x ) = \frac { 1 } { 2 }$ while $\lim _ { x \rightarrow 1 ^ { - } }f ^ { \prime } ( x ) = 2 , f ( x )$ is not differentiable at $x = 1$ .
D) Since $\lim _ { x \rightarrow 1 ^ { + } } f ^ { \prime } ( x ) = 2$ while $\lim _ { x \rightarrow 1 ^ { - } } f ^ { \prime } ( x ) = 2 , f ( x )$ is differentiable at $x = 1$ .