Multiple Choice
Select the graph of the polar equation using symmetry, zeros, maximum r-values, and any other additional points.
A)
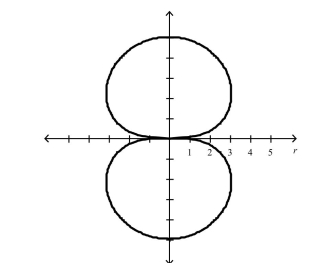
B)
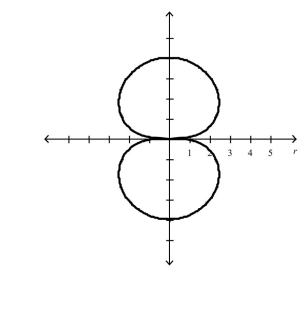
C)

D)
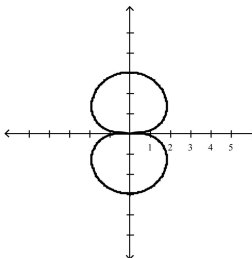
E)
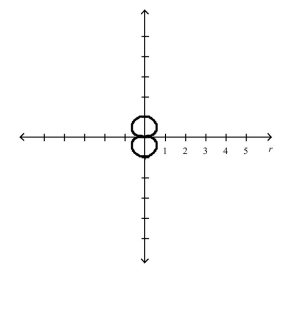
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q22: Identify the conic as a circle
Q23: Find the standard form of the
Q24: Select the graph for following equation.
Q25: Using following result find a set
Q26: Select the graph of the following
Q28: Convert the polar equation to rectangular
Q29: Find a polar equation of the
Q30: Find the standard form of the
Q31: Consider a line with slope m
Q32: Find the standard form of the