Multiple Choice
Select the parametric equations matching with the following graph. 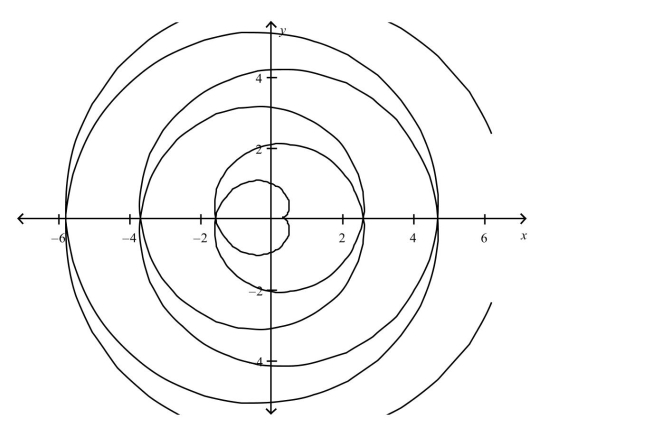
A)
Involute of circle:
B)
Involute of circle:
C)
Involute of circle:
D) Involute of circle:
E)
Involute of circle:
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q42: Find the standard form of the
Q43: By using a graphing utility select
Q44: Select the graph of the polar
Q45: Find the Eccentricity of the conic.
Q46: Select the graph of the equation
Q48: Select the graph of the polar
Q49: Find the standard form of the
Q50: Select the graph of the polar
Q51: A point in polar coordinates is
Q52: Convert the polar equation to rectangular