Solved

Solve the Problem. -A Rectangular Enclosure Must Have an Area of at Least

Question 54

Multiple Choice

Solve the problem.
-A rectangular enclosure must have an area of at least Solve the problem. -A rectangular enclosure must have an area of at least If 260 yd of fencing is to be used, and the width cannot exceed the length, within what limits must the width of the enclosure lie? A) B) C) D) If 260 yd of fencing is to be used, and the width cannot exceed the length, within what limits must the width of the enclosure lie?


A) Solve the problem. -A rectangular enclosure must have an area of at least If 260 yd of fencing is to be used, and the width cannot exceed the length, within what limits must the width of the enclosure lie? A) B) C) D)
B) Solve the problem. -A rectangular enclosure must have an area of at least If 260 yd of fencing is to be used, and the width cannot exceed the length, within what limits must the width of the enclosure lie? A) B) C) D)
C) Solve the problem. -A rectangular enclosure must have an area of at least If 260 yd of fencing is to be used, and the width cannot exceed the length, within what limits must the width of the enclosure lie? A) B) C) D)
D) Solve the problem. -A rectangular enclosure must have an area of at least 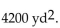If 260 yd of fencing is to be used, and the width cannot exceed the length, within what limits must the width of the enclosure lie? A) B) 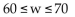C) 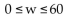D)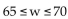

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q49: Use transformations to graph the function and

Q50: Sketch a graph to represent the situation

Q51: Solve the problem.<br>-Ken is 6 feet tall

Q52: Determine whether or not the function is

Q53: Graph the equation by plotting ordered pairs

Q55: Find the inverse of the function.<br>-f(x) =

Q56: Evaluate.<br>-Given f(x) = 4x + 4 and

Q57: Find the domain and range.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8458/.jpg" alt="Find

Q58: Find the domain and range.<br>-y = <img

Q59: Evaluate.<br>-If f = (2, -6), (5, -3),