Solve the Problem. -Ken Is 6 Feet Tall and Is Walking Away from Walking

Multiple Choice

Solve the problem.
-Ken is 6 feet tall and is walking away from a streetlight. The streetlight has its light bulb 14 feet above the ground, and Ken is walking at the rate of 5.2 feet per second. Find a function, d(t) , which gives the distance Ken
Is from the streetlight in terms of time. Find a function, S(d) , which gives the length of Ken's shadow in terms of
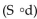D. Then find (t) . What is the meaning of (t) ?

A) 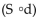(t) gives the distance Ken is from the streetlight in terms of time.
B) (t) gives the length of Ken's shadow in terms of time.
C) 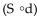(t) gives the length of Ken's shadow in terms of his distance from the streetlight.
D) 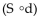(t) gives the time in terms of Ken's distance from the streetlight.