Multiple Choice
Solve the inequality. Graph the solution set and write it using interval notation.
A) ;
B) ;
C) ;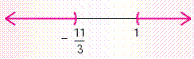
D) ;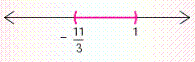
E) no solution; 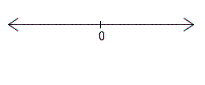
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q167: Which of the following statements is
Q168: Let <span class="ql-formula" data-value="A =
Q169: Write the system of inequalities which
Q170: Is the boundary line of
Q171: Company A offers a monthly salary of
Q173: What is incorrect about the following
Q174: Solve the inequality and graph the
Q175: Solve the equation. <span class="ql-formula"
Q176: Solve the inequality <span class="ql-formula"
Q177: Solve the compound inequality. Graph the