Multiple Choice
Graph the solution to the inequality on the real number line.
A) 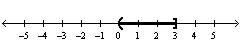
B) 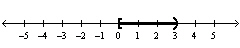
C) 
D) 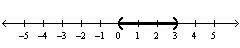
E) none of these
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q85: If the perimeter of a rectangle is
Q86: Use a graphing calculator to approximate
Q87: Write the quadratic equation having solutions
Q88: Find all real and complex solutions
Q89: The amount A in an account
Q91: Solve the equation <span class="ql-formula"
Q92: Find the vertex of <span
Q93: Graph the solution to the inequality
Q94: Solve the equation <span class="ql-formula"
Q95: Solve the equation <span class="ql-formula"