Solved

Suppose That a Is an Matrix and Is

Question 22

True/False

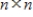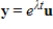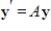Suppose that A is an Suppose that A is an matrix and is a solution to the system of linear differential equations where is an eigenvector of A with associated eigenvalue . Let k be any scalar. Then is a solution to the system . matrix and Suppose that A is an matrix and is a solution to the system of linear differential equations where is an eigenvector of A with associated eigenvalue . Let k be any scalar. Then is a solution to the system . 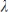is a solution to the system of linear differential equations Suppose that A is an matrix and is a solution to the system of linear differential equations where is an eigenvector of A with associated eigenvalue . Let k be any scalar. Then is a solution to the system . where Suppose that A is an matrix and is a solution to the system of linear differential equations where is an eigenvector of A with associated eigenvalue . Let k be any scalar. Then is a solution to the system . is an eigenvector of A with associated eigenvalue Suppose that A is an matrix and is a solution to the system of linear differential equations where is an eigenvector of A with associated eigenvalue . Let k be any scalar. Then is a solution to the system .
. Let k be any scalar. Then Suppose that A is an matrix and is a solution to the system of linear differential equations where is an eigenvector of A with associated eigenvalue . Let k be any scalar. Then is a solution to the system . is a solution to the system Suppose that A is an matrix and is a solution to the system of linear differential equations where is an eigenvector of A with associated eigenvalue . Let k be any scalar. Then is a solution to the system .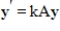
.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q17: Compute <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="Compute if

Q18: Find the eigenvalues and a basis for

Q19: Determine the rotation and dilation that result

Q20: Determine which of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="Determine which

Q21: The matrix <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="The matrix

Q23: The Power Method applied to the matrix

Q24: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="If is

Q25: Factor the matrix <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="Factor the

Q26: If A is diagonalizable, then <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg"

Q27: Find the characteristic polynomial, the eigenvalues, and