Solved

Compute the First Two Iterations of the Shifted Inverse Power

Question 29

Essay

Compute the first two iterations of the Shifted Inverse Power Method, starting with the given Compute the first two iterations of the Shifted Inverse Power Method, starting with the given , to determine the eigenvalue of A closest to , rounding any numerical values to two decimal places. , to determine the eigenvalue of A closest to Compute the first two iterations of the Shifted Inverse Power Method, starting with the given , to determine the eigenvalue of A closest to , rounding any numerical values to two decimal places. , rounding any numerical values to two decimal places.
Compute the first two iterations of the Shifted Inverse Power Method, starting with the given 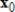, to determine the eigenvalue of A closest to 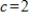, rounding any numerical values to two decimal places.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q24: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="If is

Q25: Factor the matrix <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="Factor the

Q26: If A is diagonalizable, then <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg"

Q27: Find the characteristic polynomial, the eigenvalues, and

Q28: Diagonalize the matrix A, if possible.<br> <img

Q30: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="If is

Q31: The coefficient matrix for a system of

Q32: The Inverse Power Method applied to the

Q33: The coefficient matrix for a system of

Q34: Find the matrix A that has the