Consider the Following Two Two-Player Games - Game 1 and Game

Not Answered

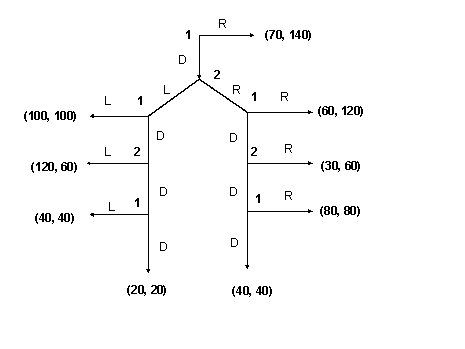
Consider the following two two-player games - Game 1 and Game 2. In each game, 1 and 2 refer to the two players. The first number in each payoff box refers to the payoff for player 1 and the second number to the payoff for player 2. The strategies L, R, and D stand for Left, Right and Down respectively. At each node I have shown the player who gets to move at that node.
Game 1:
Game 2:
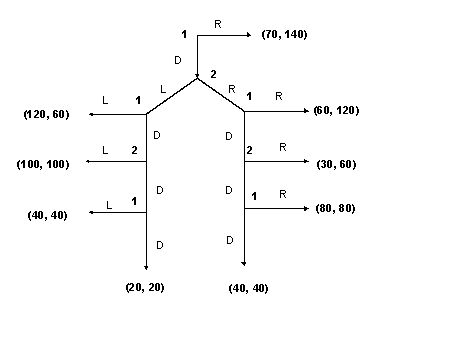(a) What is the subgame perfect equilibrium in Game 1 and Game 2? (It is the same in both games. So you only need to solve for it once.) (b) In which game - 1 or 2 - is the symmetric joint payoff maximizing outcome of (100, 100) more likely? Is it Game 1 or Game 2? Why? Explain briefly.