Determine Whether the Set of All First-Degree Polynomial Functions as Given

Multiple Choice

Determine whether the set of all first-degree polynomial functions as given below, whose graphs pass through the origin with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails.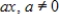

A) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
D) This set is a vector space. All ten vector space axioms hold.
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication