Solved

Determine Whether Is a Basis for

Question 16

Multiple Choice

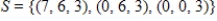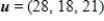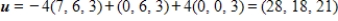
Determine whether Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and C) S is a basis for and D) S is a basis for and E) S is not a basis for is a basis for Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and C) S is a basis for and D) S is a basis for and E) S is not a basis for . 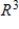If it is, write Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and C) S is a basis for and D) S is a basis for and E) S is not a basis for as a linear combination of the vectors in S.?


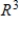A) S is a basis for Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and C) S is a basis for and D) S is a basis for and E) S is not a basis for and Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and C) S is a basis for and D) S is a basis for and E) S is not a basis for
B) S is a basis for Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and C) S is a basis for and D) S is a basis for and E) S is not a basis for and Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and C) S is a basis for and D) S is a basis for and E) S is not a basis for
C) S is a basis for Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and C) S is a basis for and D) S is a basis for and E) S is not a basis for and Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and C) S is a basis for and D) S is a basis for and E) S is not a basis for
D) S is a basis for Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and C) S is a basis for and D) S is a basis for and E) S is not a basis for and Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and C) S is a basis for and D) S is a basis for and E) S is not a basis for
E) S is not a basis for Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and C) S is a basis for and D) S is a basis for and 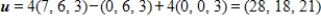E) S is not a basis for

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q11: Provided <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="Provided and

Q12: the following subset of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="the

Q13: Given that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="Given that

Q14: Determine whether the set of all third-degree

Q15: The set <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="The set

Q17: Determine whether the set of all first-degree

Q18: Write the standard basis for the vector

Q19: The set of all <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="The

Q20: Given that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="Given that

Q21: Find the Wronskian for the set of