Short Answer
Formulate the following problem as a linear programming problem (DO NOT SOLVE):A small accounting firm prepares tax returns for two types of customers: individuals and small businesses. Data is collected during an interview. A computer system is used to produce the tax return. It takes 2.5 hours to enter data into the computer for an individual tax return and 3 hours to enter data for a small business tax return. There is a maximum of 40 hours per week for data entry. It takes 20 minutes for the computer to process an individual tax return and 30 minutes to process a small business tax return. The computer is available for a maximum of 900 minutes per week. The accounting firm makes a profit of $125 on each individual tax return processed and a profit of $210 on each small business tax return processed. How many of each type of tax return should the firm schedule each week in order to maximize its profit? (Let 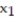 equal the number of individual tax returns and
equal the number of individual tax returns and 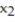 the number of small business tax returns.)
the number of small business tax returns.)
Graph the constant-profit lines through (3, 2) and (5, 3). Use a straightedge to identify the corner point(s) where the maximum profit occurs for the given objective function. 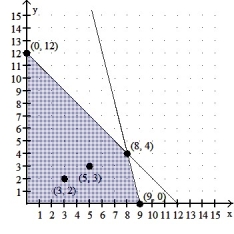
Correct Answer:

Verified
Correct Answer:
Verified
Q1: Use graphical methods to solve the linear
Q2: Graph the inequality:<br>-y < - 2 <img
Q3: The corner points for the bounded feasible
Q4: Graph the solution set of the system
Q6: The corner points for the bounded feasible
Q7: Formulate the following problem as a linear
Q8: Graph the inequality:<br>-2x + y
Q9: Use graphical methods to solve the linear
Q10: Graph the inequality:<br>-4x - 2y <span
Q11: Solve the following linear programming problem by