Formulate the Following Problem as a Linear Programming Problem (DO

Short Answer

Formulate the following problem as a linear programming problem (DO NOT SOLVE):A dietitian can purchase an ounce of chicken for $0.25 and an ounce of potatoes for $0.02. Each ounce of chicken contains 13 units of protein and 24 units of carbohydrates. Each ounce of potatoes contains 5 units of protein and 35 units of carbohydrates. The minimum daily requirements for the patients under the dietitian's care are 45 units of protein and 58 units of carbohydrates. How many ounces of each type of food should the dietitian purchase for each patient so as to minimize costs and at the same time insure the minimum daily requirements of protein and carbohydrates? (Let 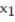equal the number of ounces of chicken and 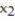the number of ounces of potatoes purchased per patient.)