Multiple Choice
The Laplace transform of F(t) = cos(3t) H(t - /2) is equal to
A) 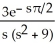
B) 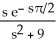
C) 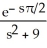
D) 
E) - 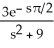
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q74: Find the general solution of the differential
Q75: Find the general solution of the differential
Q76: Solve the following initial-value problem:cos(x) <img
Q77: Given that y = x is a
Q78: Find the general solution of the differential
Q80: Solve the initial-value problem ( <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q81: Solve the initial-value problem x <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q82: Find a general solution of the first
Q83: Find the general solution of the differential
Q84: Use Euler's method with step size h