Solved

Solve the Initial-Value Problem ( - 1)

Question 80

Multiple Choice

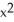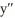Solve the initial-value problem ( Solve the initial-value problem ( - 1) + x - y = 0, y(0) = 1, (0) = 0 in the form of a power series in powers of x. A) 1 - B) 1 - C) 1 - D) 1 + E) 1 + - 1) Solve the initial-value problem ( - 1) + x - y = 0, y(0) = 1, (0) = 0 in the form of a power series in powers of x. A) 1 - B) 1 - C) 1 - D) 1 + E) 1 + + x Solve the initial-value problem ( - 1) + x - y = 0, y(0) = 1, (0) = 0 in the form of a power series in powers of x. A) 1 - B) 1 - C) 1 - D) 1 + E) 1 + - y = 0, y(0) = 1, Solve the initial-value problem ( - 1) + x - y = 0, y(0) = 1, (0) = 0 in the form of a power series in powers of x. A) 1 - B) 1 - C) 1 - D) 1 + E) 1 + (0) = 0 in the form of a power series in powers of x.


A) 1 - Solve the initial-value problem ( - 1) + x - y = 0, y(0) = 1, (0) = 0 in the form of a power series in powers of x. A) 1 - B) 1 - C) 1 - D) 1 + E) 1 + Solve the initial-value problem ( - 1) + x - y = 0, y(0) = 1, (0) = 0 in the form of a power series in powers of x. A) 1 - B) 1 - C) 1 - D) 1 + E) 1 +
B) 1 - Solve the initial-value problem ( - 1) + x - y = 0, y(0) = 1, (0) = 0 in the form of a power series in powers of x. A) 1 - B) 1 - C) 1 - D) 1 + E) 1 + Solve the initial-value problem ( - 1) + x - y = 0, y(0) = 1, (0) = 0 in the form of a power series in powers of x. A) 1 - B) 1 - C) 1 - D) 1 + E) 1 +
C) 1 - Solve the initial-value problem ( - 1) + x - y = 0, y(0) = 1, (0) = 0 in the form of a power series in powers of x. A) 1 - B) 1 - C) 1 - D) 1 + E) 1 + Solve the initial-value problem ( - 1) + x - y = 0, y(0) = 1, (0) = 0 in the form of a power series in powers of x. A) 1 - B) 1 - C) 1 - D) 1 + E) 1 +
D) 1 + Solve the initial-value problem ( - 1) + x - y = 0, y(0) = 1, (0) = 0 in the form of a power series in powers of x. A) 1 - B) 1 - C) 1 - D) 1 + E) 1 + Solve the initial-value problem ( - 1) + x - y = 0, y(0) = 1, (0) = 0 in the form of a power series in powers of x. A) 1 - B) 1 - C) 1 - D) 1 + E) 1 +
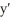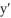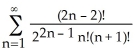
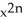
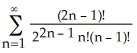
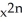
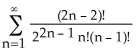
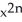
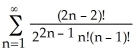
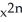
E) 1 + Solve the initial-value problem ( - 1) + x - y = 0, y(0) = 1, (0) = 0 in the form of a power series in powers of x. A) 1 - B) 1 - C) 1 - D) 1 + E) 1 + Solve the initial-value problem ( - 1) + x - y = 0, y(0) = 1, (0) = 0 in the form of a power series in powers of x. A) 1 - B) 1 - C) 1 - D) 1 + E) 1 +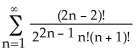

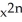
Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q75: Find the general solution of the differential

Q76: Solve the following initial-value problem:cos(x) <img

Q77: Given that y = x is a

Q78: Find the general solution of the differential

Q79: The Laplace transform of F(t) =

Q81: Solve the initial-value problem x <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"

Q82: Find a general solution of the first

Q83: Find the general solution of the differential

Q84: Use Euler's method with step size h

Q85: Find an integrating factor of the form