Multiple Choice
You probably know by now that a differential k-form k 1 on a domain D 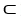
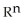 is very similar to a vector field on D, and hence a correspondence between the two may be established.For instance, we may set a correspondence between the 1-form
is very similar to a vector field on D, and hence a correspondence between the two may be established.For instance, we may set a correspondence between the 1-form 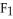 dx +
dx + 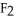 dy +
dy + 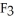 dz and the vector field F =
dz and the vector field F =  i +
i + 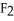 j +
j + 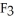 k. Using this setup, find the vector differential identity corresponding to the fact
k. Using this setup, find the vector differential identity corresponding to the fact 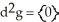 for any differential 0-form g on a domain D in
for any differential 0-form g on a domain D in  .
.
A) . ( g) = 0
B) × ( g) = 0
C) 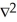 (g) = 0
(g) = 0
D) g = 0
E) ( g) . ) = 0
Correct Answer:

Verified
Correct Answer:
Verified
Q45: Which of the following is an antiderivative
Q46: Let F(x, y) and G(x, y) be
Q47: Find the dimension of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find
Q48: Let Ω be the
Q49: Let g(x) be a differential 0-form
Q51: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="If is
Q52: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let be
Q53: Evaluate the integral of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q54: Find the 2-volume of the 2-manifold
Q55: Let Φ = (2xy - <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"