Solved

Let the Differential 2-Form = Dz

Question 67

Multiple Choice

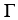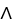Let the differential 2-form Let the differential 2-form = xdy dz + ydz dx + (1 - 2z) dx dy be defined in a star-like domain . (a) Is closed? (b) Is exact on D? If so, find a differential 1-form such that = d . A) is neither closed nor exact B) is both closed and exact, = ydx + 2xzdy - xydz C) is closed but not exact D) is exact but not closed, = ydx + 2xzdy + xydz E) is both closed and exact, = -ydx - 2xzdy - xydz = xdyLet the differential 2-form = xdy dz + ydz dx + (1 - 2z) dx dy be defined in a star-like domain . (a) Is closed? (b) Is exact on D? If so, find a differential 1-form such that = d . A) is neither closed nor exact B) is both closed and exact, = ydx + 2xzdy - xydz C) is closed but not exact D) is exact but not closed, = ydx + 2xzdy + xydz E) is both closed and exact, = -ydx - 2xzdy - xydz dz + ydz11ee7bc9_e7ae_ceff_ae82_cb591a35a817_TB9661_11 dx + (1 - 2z) dx11ee7bc9_e7ae_ceff_ae82_cb591a35a817_TB9661_11 dy be defined in a star-like domain 11ee77e1_7790_a948_a0f8_3be4758d6c01_TB9661_11 .
(a) Is 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 closed?
(b) Is 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 exact on D? If so, find a differential 1-form 11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11 such that 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 = d11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11.


A) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is neither closed nor exact
B) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is both closed and exact, 11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11 = ydx + 2xzdy - xydz
C) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is closed but not exact
D) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is exact but not closed, 11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11 = ydx + 2xzdy + xydz
E) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is both closed and exact, 11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11 = -ydx - 2xzdy - xydz

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q62: Let S be a piece with boundary

Q63: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let

Q64: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" A) u .

Q65: Calculate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Calculate

Q66: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let =

Q68: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let ,

Q69: State the Divergence Theorem and Stokes's Theorem

Q70: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let ,

Q71: Let e<sub>i</sub> , i = 1, 2,

Q72: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find ,