Let S Be a Piece with Boundary of a Smooth

Multiple Choice

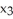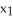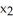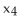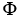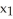
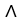Let S be a piece with boundary of a smooth 3-manifold in R⁴ (hypersurface) given by the equation = g( , , ) and let= d d 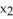11ee7bcb_c6fc_6099_ae82_719973faadb8_TB9661_11 d 11ee77e1_7793_6815_a0f8_474d4dbcd8a5_TB9661_11 . Apart from sign due to orientation of S, 11ee77e1_7793_6816_a0f8_97457d751d61_TB9661_11 is equal to

A) the 3-volume of the projection of S onto the hyperplane 11ee77e1_7793_6817_a0f8_13032b247b87_TB9661_11 = 0
B) the 4-volume of the projection of S onto the hyperplane 11ee77e1_7793_6818_a0f8_43b7fef76a07_TB9661_11 = 0
C) 11ee77e1_7793_6819_a0f8_5d277b36f478_TB9661_11
D) 11ee77e1_7793_681a_a0f8_d78a3ae2089d_TB9661_11
E) None of the above