The 2-Manifold M in R⁴ given by the Equations

Multiple Choice

The 2-manifold M in R⁴ given by the equations 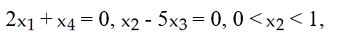0 < x₄ < 1,
0 < < 1 has normals 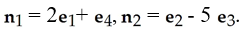It is oriented by the 2-form
ω(x) ( v₁ , v₂ ) = det( n₁ n₂ v₁ v₂ ) . Let be a parametrization for M. Which of the following statements is true?

A) P is orientation preserving for M.
B) P does not determine an orientation for M.
C) P is orientation reversing for M, but no orientation preserving parametrization for M exists.
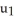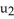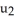D) P is orientation reversing for M, but q(u) = ( , 5 , , -2 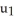) would be orientation preserving parametrization for M.
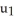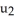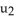E) P is orientation reversing for M, but q(u) = (- , 5 , , 2 ) would be an orientation-preserving parametrization for M.