Multiple Choice
You probably know by now that a differential k-form k 1 on a domain D 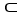
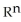 is very similar to a vector field on D, and hence a correspondence between the two may be established.Let
is very similar to a vector field on D, and hence a correspondence between the two may be established.Let 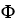 = F dx + G dy + H dz be a differential 1-form on a domain D
= F dx + G dy + H dz be a differential 1-form on a domain D 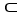
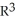 and let
and let 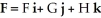 be the vector field corresponding to 11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 . Using this set up, find the vector differential identity corresponding to the fact 11ee77e1_778f_e5c1_a0f8_85abfcfe325a_TB9661_11 11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 = 11ee77e1_778f_e5c2_a0f8_6b21bea3e968_TB9661_11 .
be the vector field corresponding to 11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 . Using this set up, find the vector differential identity corresponding to the fact 11ee77e1_778f_e5c1_a0f8_85abfcfe325a_TB9661_11 11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 = 11ee77e1_778f_e5c2_a0f8_6b21bea3e968_TB9661_11 .
A) (divF) = 0
B) curl(F) = 0
C) div(curl F) = 0
D) 11ee77e1_778f_e5c3_a0f8_d591926a725c_TB9661_11 F = 0
E) curl(curl F) = 0
Correct Answer:

Verified
Correct Answer:
Verified
Q56: The 2-manifold M in R<sup>4 </sup>given
Q57: Let C be the curve of
Q58: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let (
Q59: Use the generalized Stokes's Theorem to
Q60: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" If
Q62: Let S be a piece with boundary
Q63: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let
Q64: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" A) u .
Q65: Calculate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Calculate
Q66: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let =