Find the Flux of F = Out of (A) $\le$

Multiple Choice

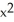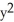
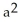Find the flux of F = out of (a) the disk + $\le$ , (b) an arbitrary plane region not containing the origin in its interior or on its boundary, and (c) an arbitrary plane region containing the origin in its interior.

A) (a) 0 $~~~~~~~~$ (b) 0 $~~~~~~~~$ (c) 0
B) (a) 2 $\pi$ $~~~~~~~~$ (b) 0 $~~~~~~~~$ (c) 2 $\pi$
C) (a) 2 $\pi$ a $~~~~~~~~$ (b) 0 $~~~~~~~~$ (c) 2 $\pi$
D) (a) 0 $~~~~~~~~$ (b) 2 $\pi$ $~~~~~~~~$ (c) 0
E) None of the above