Multiple Choice
A potential function of a vector field F is given by 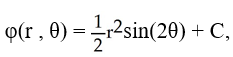 , where (r , θ) are the polar coordinates and C is an arbitrary constant. Find F.
, where (r , θ) are the polar coordinates and C is an arbitrary constant. Find F.
Hint: The gradient of g(r , θ) is given by ∇g(r , θ) = 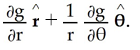 .
.
A) r sin(2 ) + r cos(2 )
B) r sin(2 )  + r cos(2 )
+ r cos(2 ) 
C) r sin(2 )  - r cos(2 )
- r cos(2 ) 
D) r sin(2 )  +
+  r cos(2 )
r cos(2 ) 
E) r sin(2 ) - r cos(2 )
Correct Answer:

Verified
Correct Answer:
Verified
Q8: Let C be the curve of
Q9: Integrate g(x, y, z) = x<sup>2</sup>y<sup>2</sup>z<sup>2</sup> over
Q10: Find the area of the ellipse
Q11: Show that the fixed point at the
Q12: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate the
Q14: Compute the flux of F = x
Q15: Describe the streamlines of the given velocity
Q16: Is F (x,y,z) = 6xy sin(2z) i
Q17: Evaluate the line integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate
Q18: Find the work done by the