Multiple Choice
Integrate g(x, y, z) = x2y2z2 over the surface of the rectangular solid cut from the first octant by the planes x = a, y = b, and z = c.
A) 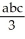 (ab + ac + bc)
(ab + ac + bc)
B) 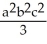 (ab + ac + bc)
(ab + ac + bc)
C) 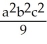 (ab + ac + bc)
(ab + ac + bc)
D) 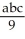 (ab + ac + bc)
(ab + ac + bc)
E) abc(ab + ac + bc)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q4: The Liapunov function V(x,y) = 2 <img
Q5: Find the work done by the force
Q6: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Find
Q7: Evaluate the surface integral <img
Q8: Let C be the curve of
Q10: Find the area of the ellipse
Q11: Show that the fixed point at the
Q12: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate the
Q13: A potential function of a vector
Q14: Compute the flux of F = x