Multiple Choice
Find 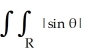 dA, where R is the region outside the circle r = 1 and inside the cardioid r = 1 + cos .
dA, where R is the region outside the circle r = 1 and inside the cardioid r = 1 + cos .
A) 
B) 
C) 
D) 
E) 
Correct Answer:

Verified
Correct Answer:
Verified
Q1: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate the
Q2: Let J = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="
Q3: Use a suitable change of variables to
Q4: Use a triple integral iterated in
Q6: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Evaluate
Q7: Find the volume remaining after a
Q8: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate ,
Q9: Evaluate the iterated integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q10: Let D be the planar region occupied
Q11: Evaluate the iterated integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate