Multiple Choice
Use a triple integral iterated in spherical coordinates to find the volume of the region lying above the cone 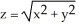 and inside the sphere x2 + y2 + z2 = a2.
and inside the sphere x2 + y2 + z2 = a2.
A) 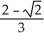
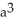 cubic units
cubic units
B) 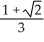
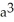 cubic units
cubic units
C) 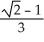
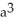 cubic units
cubic units
D) 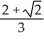
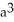 cubic units
cubic units
E) 
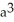 cubic units
cubic units
Correct Answer:

Verified
Correct Answer:
Verified
Q1: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate the
Q2: Let J = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="
Q3: Use a suitable change of variables to
Q5: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Find
Q6: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Evaluate
Q7: Find the volume remaining after a
Q8: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate ,
Q9: Evaluate the iterated integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q10: Let D be the planar region occupied
Q11: Evaluate the iterated integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate