Solved

Find and Classify the Critical Points of the Following Function

Question 37

Multiple Choice

Find and classify the critical points of the following function: f(x, y) = 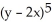Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) + 30x3 - 15y3.


A) saddle points are ( Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) , - Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) ) and (- Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) , Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) ) , maximum at (3, 3) and minimum at (-3, -3)
B) saddle points are (0, 0) , ( Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) , - Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) ) and (- Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) , Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) ) , minimum at (3, 3) and maximum at (-3, -3)
C) saddle points are (0, 0) , ( Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) , - Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) ) , (- Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) , Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) ) , (3, 3) , and (-3, -3)
D) saddle points are (0, 0) , ( Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) , - Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) ) and (- Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) , Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) ) , maximum at (3, 3) and minimum at (-3, -3)
E) saddle points are (0, 0) , ( Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) , - Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) ) and (- Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) , Find and classify the critical points of the following function: f(x, y) = + 30x<sup>3</sup> - 15y<sup>3</sup>. A) saddle points are ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) B) saddle points are (0, 0) , ( , - ) and (- , ) , minimum at (3, 3) and maximum at (-3, -3) C) saddle points are (0, 0) , ( , - ) , (- , ) , (3, 3) , and (-3, -3) D) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, 3) and minimum at (-3, -3) E) saddle points are (0, 0) , ( , - ) and (- , ) , maximum at (3, -3) and minimum at (-3, 3) ) , maximum at (3, -3) and minimum at (-3, 3)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q32: Find and classify the critical points of

Q33: If a function f(x,y) has a local

Q34: Find and classify all critical points for

Q35: Find the absolute maximum and minimum

Q36: Find and classify all critical points of

Q38: Find the derivative of the function f(x)

Q39: If the Lagrange function L corresponding to

Q40: By first differentiating the integral, evaluate <img

Q41: (i) Maximize <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="(i) Maximize

Q42: Find the maximum and minimum values of