Solved

Find the Absolute Maximum and Minimum Values of F(x, Y

Question 67

Multiple Choice

Find the absolute maximum and minimum values of f(x, y, z) = xyz(1 - x2 - y2 - z2) on the tetrahedron bounded by x = 0, y = 0, z = 0, and x + y + z = 2.


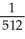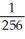A) maximum Find the absolute maximum and minimum values of f(x, y, z) = xyz(1 - x<sup>2</sup> - y<sup>2</sup> - z<sup>2</sup>) on the tetrahedron bounded by x = 0, y = 0, z = 0, and x + y + z = 2. A) maximum , minimum 0 B) maximum , minimum 0 C) maximum , minimum 0 D) maximum , minimum 0 E) none of the above , minimum 0
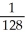B) maximum Find the absolute maximum and minimum values of f(x, y, z) = xyz(1 - x<sup>2</sup> - y<sup>2</sup> - z<sup>2</sup>) on the tetrahedron bounded by x = 0, y = 0, z = 0, and x + y + z = 2. A) maximum , minimum 0 B) maximum , minimum 0 C) maximum , minimum 0 D) maximum , minimum 0 E) none of the above , minimum 0
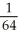C) maximum Find the absolute maximum and minimum values of f(x, y, z) = xyz(1 - x<sup>2</sup> - y<sup>2</sup> - z<sup>2</sup>) on the tetrahedron bounded by x = 0, y = 0, z = 0, and x + y + z = 2. A) maximum , minimum 0 B) maximum , minimum 0 C) maximum , minimum 0 D) maximum , minimum 0 E) none of the above , minimum 0
D) maximum Find the absolute maximum and minimum values of f(x, y, z) = xyz(1 - x<sup>2</sup> - y<sup>2</sup> - z<sup>2</sup>) on the tetrahedron bounded by x = 0, y = 0, z = 0, and x + y + z = 2. A) maximum , minimum 0 B) maximum , minimum 0 C) maximum , minimum 0 D) maximum , minimum 0 E) none of the above , minimum 0
E) none of the above

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q57: Find the maximum and minimum values

Q58: Find and classify all critical points for

Q59: Use Lagrange multipliers to find the maximum

Q60: Find and classify the critical points of

Q61: Find the empirical regression line y =

Q62: Find the absolute maximum and minimum

Q63: Find the maximum and minimum values of

Q64: Find the envelope of the family of

Q65: Find the values of constant real numbers

Q66: Find the absolute maximum and minimum