Multiple Choice
Find the two unit vectors tangent at the point (1, 1, 1) to the curve of intersection of the surfaces xy2 + x2y + z3 = 3 and x3 - y3 - xyz = -1.
A) ± 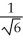 ( i + j - 2 k )
( i + j - 2 k )
B) ±  ( i - j - 2 k )
( i - j - 2 k )
C) ±  ( i - 2 j - 2 k )
( i - 2 j - 2 k )
D) ± 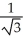 ( i + j - k )
( i + j - k )
E) ± 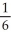 ( i + j - 2 k )
( i + j - 2 k )
Correct Answer:

Verified
Correct Answer:
Verified
Q44: Let g be a function of a
Q45: Describe the level curves of the function
Q46: Find the equation of the normal line
Q47: Assume that the relation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Assume
Q48: The graph below shows level curves f(x,y)
Q50: Identify the function f(x,y) whose domain is
Q51: Find an equation of the plane tangent
Q52: Given z = f(x, y) = <img
Q53: Assuming that the function f has continuous
Q54: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" A)