Solved

Assume That the Relation - 65 + =

Question 47

Essay

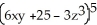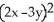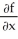Assume that the relation Assume that the relation - 65 + = 0 defines z as a differentiable functionof x and y near the point (x , y) = (4 , 0). (a) If z = f(x , y) , find and at (x,y) = (4 , 0). (b) If x = + , y = , find at (u , v) =(0 , 2)\. Hints :Part (a): First , find the value of z at (x , y) =(4 , 0). Part (b): Use the chain rule! - 65 + Assume that the relation - 65 + = 0 defines z as a differentiable functionof x and y near the point (x , y) = (4 , 0). (a) If z = f(x , y) , find and at (x,y) = (4 , 0). (b) If x = + , y = , find at (u , v) =(0 , 2)\. Hints :Part (a): First , find the value of z at (x , y) =(4 , 0). Part (b): Use the chain rule! = 0 defines z as a differentiable functionof x and y near the point (x , y) = (4 , 0).
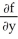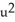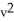(a) If z = f(x , y) , find Assume that the relation - 65 + = 0 defines z as a differentiable functionof x and y near the point (x , y) = (4 , 0). (a) If z = f(x , y) , find and at (x,y) = (4 , 0). (b) If x = + , y = , find at (u , v) =(0 , 2)\. Hints :Part (a): First , find the value of z at (x , y) =(4 , 0). Part (b): Use the chain rule! and Assume that the relation - 65 + = 0 defines z as a differentiable functionof x and y near the point (x , y) = (4 , 0). (a) If z = f(x , y) , find and at (x,y) = (4 , 0). (b) If x = + , y = , find at (u , v) =(0 , 2)\. Hints :Part (a): First , find the value of z at (x , y) =(4 , 0). Part (b): Use the chain rule! at (x,y) = (4 , 0).
(b) If x = Assume that the relation - 65 + = 0 defines z as a differentiable functionof x and y near the point (x , y) = (4 , 0). (a) If z = f(x , y) , find and at (x,y) = (4 , 0). (b) If x = + , y = , find at (u , v) =(0 , 2)\. Hints :Part (a): First , find the value of z at (x , y) =(4 , 0). Part (b): Use the chain rule! + Assume that the relation - 65 + = 0 defines z as a differentiable functionof x and y near the point (x , y) = (4 , 0). (a) If z = f(x , y) , find and at (x,y) = (4 , 0). (b) If x = + , y = , find at (u , v) =(0 , 2)\. Hints :Part (a): First , find the value of z at (x , y) =(4 , 0). Part (b): Use the chain rule! , y = Assume that the relation - 65 + = 0 defines z as a differentiable functionof x and y near the point (x , y) = (4 , 0). (a) If z = f(x , y) , find and at (x,y) = (4 , 0). (b) If x = + , y = , find at (u , v) =(0 , 2)\. Hints :Part (a): First , find the value of z at (x , y) =(4 , 0). Part (b): Use the chain rule! , find Assume that the relation - 65 + = 0 defines z as a differentiable functionof x and y near the point (x , y) = (4 , 0). (a) If z = f(x , y) , find and at (x,y) = (4 , 0). (b) If x = + , y = , find at (u , v) =(0 , 2)\. Hints :Part (a): First , find the value of z at (x , y) =(4 , 0). Part (b): Use the chain rule! at (u , v) =(0 , 2)\.
Hints :Part (a): First , find the value of z at (x , y) =(4 , 0).
Part (b): Use the chain rule!

Correct Answer:

verifed

Verified

(a) blured image = blured image , ...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q42: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find and

Q43: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find if

Q44: Let g be a function of a

Q45: Describe the level curves of the function

Q46: Find the equation of the normal line

Q48: The graph below shows level curves f(x,y)

Q49: Find the two unit vectors tangent at

Q50: Identify the function f(x,y) whose domain is

Q51: Find an equation of the plane tangent

Q52: Given z = f(x, y) = <img