Solved

Let R = R(s) Be a Curve Parametrized in Terms

Question 40

Multiple Choice

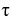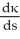Let r = r(s) be a curve parametrized in terms of arc length, let Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E) (s) and Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . 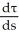A) B) C) D) E) (s) be the curvature and torsion, and let { Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . 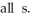A) B) C) D) E) , Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . 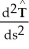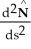A) B) C) D) E) , Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E) } be the Frenet frame for the curve. 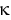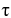Suppose that Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E) = 0 and Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E) = 0 for Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E) Calculate Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E) , Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E) , and Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E) in terms of Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E) , Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E) , Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E) , Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E) , and Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E) .


A) Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E)
B) Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E)
C) Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E)
D) Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) B) C) D) E)
E) Let r = r(s) be a curve parametrized in terms of arc length, let (s) and (s) be the curvature and torsion, and let { , , } be the Frenet frame for the curve. Suppose that = 0 and = 0 for Calculate , , and in terms of , , , , and . A) 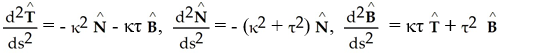B) 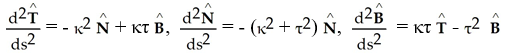C) D) 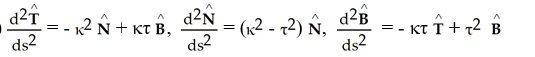E)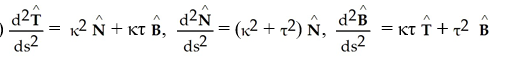

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q35: Find the radius of curvature of the

Q36: The distance from the moon to the

Q37: Find the evolute <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find the

Q38: A planet's distance from the sun at

Q39: Parametrize the parabola in which the

Q41: An object is moving to the right

Q42: The position vector of a moving particle

Q43: Find the radius of curvature of r

Q44: Find the Frenet frame for the curve

Q45: Find a parametric representation of the