Multiple Choice
Find the length of the arc y = ln(sec x) between x = 0 and x = 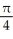 .
.
A) ln(2 + 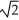 ) units
) units
B) ln(  - 1) units
- 1) units
C) ln(1 + 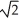 ) units
) units
D) ln(2 - 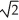 ) units
) units
E) ln(  ) units
) units
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q60: A cylindrical tank 8 m in
Q61: Use Pappus's Theorem to find the
Q62: Find the centre of mass of
Q63: For any events <span class="ql-formula"
Q64: Find the volume of a solid
Q66: Find the solution of the initial-value problem
Q67: Assuming the Earth is spherical with radius
Q68: Let A(x) be the cross-sectional area of
Q69: The region R is the portion of
Q70: The plane region bounded by the curve