Multiple Choice
Use Pappus's Theorem to find the volume of the solid of revolution obtained by rotating the triangular plane region specified by 0 y 1 -  about (a) the line x = 2 and(b) the line y = 2.
about (a) the line x = 2 and(b) the line y = 2.
A) (a) 4 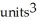 , (b)
, (b) 
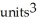
B) (a) 2 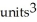 , (b)
, (b) 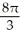
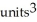
C) (a) 4 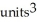 , (b)
, (b) 
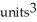
D) (a) 2 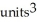 , (b)
, (b) 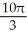
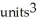
E) (a) 2  , (b)
, (b) 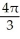
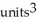
Correct Answer:

Verified
Correct Answer:
Verified
Q56: Find the moment about the x-axis
Q57: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" A)
Q58: Find the coordinates of the centroid of
Q59: Find the volume of a right circular
Q60: A cylindrical tank 8 m in
Q62: Find the centre of mass of
Q63: For any events <span class="ql-formula"
Q64: Find the volume of a solid
Q65: Find the length of the arc y
Q66: Find the solution of the initial-value problem