Solved

Apply Simpson's Rule with N = 2 to Approximate I ≤\le

Question 6

Multiple Choice

Apply Simpson's Rule with n = 2 to approximate I = 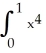Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error?


A) S2 = Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le , I - Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le = 0, estimate gives Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le ≤\le Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le
B) S2 = Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le , I - Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le = - Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? 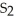A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le , estimate gives Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? 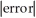A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le ≤\le Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le
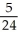C) S2 = Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? 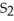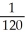A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le , I - Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? 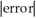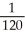A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le = Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? 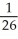A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le , estimate gives Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? 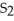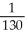A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le ≤\le Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le
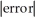
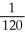
D) S2 = Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? 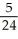A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le , I - Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? 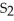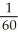A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le = - Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? 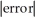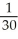A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le , estimate gives Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? 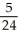A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le ≤\le Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le
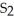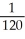E) S2 = Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? 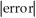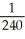A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le , I - Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le = - Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le , estimate gives Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le ≤\le Apply Simpson's Rule with n = 2 to approximate I = dx. What is the actual error in this approximation? What does the Simpson's Rule error estimate give as an upper bound for the size of the error? A) S<sub>2</sub> = , I - = 0, estimate gives \le B) S<sub>2</sub> = , I - = - , estimate gives \le C) S<sub>2</sub> = , I - = , estimate gives \le D) S<sub>2</sub> = , I - = - , estimate gives \le E) S<sub>2</sub> = , I - = - , estimate gives \le

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: Find the Trapezoid Rule approximation <img

Q2: Let f(x) = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="

Q3: Evaluate, if convergent, <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="

Q4: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="

Q5: Given that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Given that

Q7: Evaluate, if convergent, . <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"

Q8: Find the area between the curves

Q9: Evaluate the integral, <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="

Q10: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="

Q11: Find the area under the curve