Solved

The Function F(x) = ( - 5) Has

Question 128

Multiple Choice

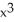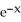The function f(x) = ( The function f(x) = ( - 5) has one critical point in the interval x > 0. Find this critical point with error within 0.005 by applying Newton's Method to an appropriate function. A) 3.4023 B) 3.2240 C) 3.1278 D) 3.4259 E) none of the above - 5) The function f(x) = ( - 5) has one critical point in the interval x > 0. Find this critical point with error within 0.005 by applying Newton's Method to an appropriate function. A) 3.4023 B) 3.2240 C) 3.1278 D) 3.4259 E) none of the above has one critical point in the interval x > 0. Find this critical point with error within 0.005 by applying Newton's Method to an appropriate function.


A) 3.4023
B) 3.2240
C) 3.1278
D) 3.4259
E) none of the above

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q120: Let g be a polynomial function such

Q121: Use Newton's Method to find the solution

Q122: Find the extreme values of f(x) =

Q123: Find a suitable linear approximation that lets

Q124: Find the equations of all horizontal asymptotes

Q125: Evaluate the limit . <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate

Q126: Find all the roots of the equation

Q127: Construct a window in the shape of

Q129: Find the Taylor polynomial of degree

Q130: Evaluate . <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Evaluate