Multiple Choice
Differentiate f(x) =  (sin(x) ) when
(sin(x) ) when 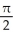 x
x 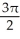 .
.
A) f'(x) = -1
B) f'(x) = -x
C) f'(x) = 1
D) f'(x) = x
E) none of the above
Correct Answer:

Verified
Correct Answer:
Verified
Q54: Solve the logarithmic equation log x =
Q55: Evaluate ln <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate ln
Q56: Let f(x) = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="
Q57: Let g be the inverse function of
Q58: Find and simplify the derivative of cosh(ln(x)).<br>A)
Q60: Find the slope of the curve <img
Q61: Solve the initial value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q62: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" A) 2x (x)
Q63: A certain radioactive isotope decays from 70
Q64: Solve the exponential equation = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"