Construct a 95% Z-Interval or a 95% T-Interval About the Population

Multiple Choice

Construct a 95% Z-interval or a 95% t-interval about the population mean. Assume the data come from a population that is approximately normal with no outliers.
-The heights of 20- to 29-year-old females are known to have a population standard deviation 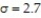inches. A simple random sample of n = 15 females 20 to 29 years old results in the following data: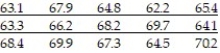

A) (65.20, 67.50) ; we are 95% confident that the mean height of 20- to 29-year-old females is between 65.20 and 67.50 inches.
B) (64.98, 67.72) ; we are 95% confident that the mean height of 20- to 29-year-old females is between 64.98 and 67.72 inches.
C) (65.12, 67.58) ; we are 95% confident that the mean height of 20- to 29-year-old females is between 65.12 and 67.58 inches.
D) (64.85, 67.85) ; we are 95% confident that the mean height of 20- to 29-year-old females is between 64.85 and 67.85 inches.