Solved

Let Be a Polynomial of Degree 5

Question 3

Multiple Choice

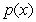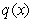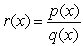Let Let be a polynomial of degree 5. Let be a polynomial of degree 4. Which of the following are true about ? A) B) C) The graph has no horizontal asymptote. D) The graph has a horizontal asymptote. be a polynomial of degree 5. Let Let be a polynomial of degree 5. Let be a polynomial of degree 4. Which of the following are true about ? A) B) C) The graph has no horizontal asymptote. D) The graph has a horizontal asymptote. be a polynomial of degree 4. Which of the following are true about Let be a polynomial of degree 5. Let be a polynomial of degree 4. Which of the following are true about ? A) B) C) The graph has no horizontal asymptote. D) The graph has a horizontal asymptote. ?


A) Let be a polynomial of degree 5. Let be a polynomial of degree 4. Which of the following are true about ? A) B) C) The graph has no horizontal asymptote. D) The graph has a horizontal asymptote.
B) Let be a polynomial of degree 5. Let be a polynomial of degree 4. Which of the following are true about ? A) B) C) The graph has no horizontal asymptote. D) The graph has a horizontal asymptote.
C) The graph has no horizontal asymptote.
D) The graph has a horizontal asymptote.

Correct Answer:

verifed

Verified

Related Questions

Q1: Suppose that a, b, c, and d

Q2: The figure below shows the graphs of

Q4: A 14 kg sample of a certain

Q5: The following figure gives the graphs of

Q6: One of the following tables of data

Q7: Find a power function through the two

Q8: A 16 kg sample of a certain

Q9: Is <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10073/.jpg" alt="Is a

Q10: The following table represents the amount of

Q11: The formula for the power function whose