Multiple Choice
Find the volume under the surface z = f(x,y) and above the rectangle with the given boundaries.
-z = 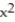 +
+ 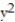 ; R = {(x, y) : 0 x 1, 0 y 1}
; R = {(x, y) : 0 x 1, 0 y 1}
A) 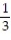
B) 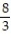
C) 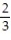
D) 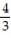
Correct Answer:

Verified
Correct Answer:
Verified
Q59: Find the average value of over the
Q60: Choose the one alternative that best completes
Q61: Find the area of the region
Q62: Choose the one alternative that best completes
Q63: Find the volume of the indicated region.<br>-the
Q65: Evaluate the integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the integral.
Q66: Find the center of mass of a
Q67: Solve the problem.<br>-Let D be the region
Q68: Evaluate the improper integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the
Q69: Evaluate the double integral over the