Solved

Solve the Problem. -Let D Be the Region That Is Bounded Below by Bounded

Question 67

Multiple Choice

Solve the problem.
-Let D be the region that is bounded below by the cone Solve the problem. -Let D be the region that is bounded below by the cone and above by the sphere Set up the triple integral for the volume of D in cylindrical coordinates. A) B) C) D) and above by the sphere Solve the problem. -Let D be the region that is bounded below by the cone and above by the sphere Set up the triple integral for the volume of D in cylindrical coordinates. A) B) C) D) Set up the triple integral for the volume of D in cylindrical coordinates.


A) Solve the problem. -Let D be the region that is bounded below by the cone and above by the sphere Set up the triple integral for the volume of D in cylindrical coordinates. A) B) C) D)
B) Solve the problem. -Let D be the region that is bounded below by the cone and above by the sphere Set up the triple integral for the volume of D in cylindrical coordinates. A) B) C) D)
C) Solve the problem. -Let D be the region that is bounded below by the cone and above by the sphere Set up the triple integral for the volume of D in cylindrical coordinates. A) B) C) D)
D) Solve the problem. -Let D be the region that is bounded below by the cone 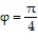and above by the sphere 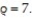Set up the triple integral for the volume of D in cylindrical coordinates. A) 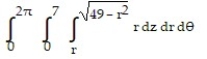B) 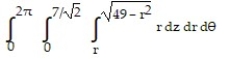C) D)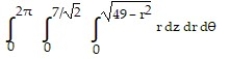

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q62: Choose the one alternative that best completes

Q63: Find the volume of the indicated region.<br>-the

Q64: Find the volume under the surface

Q65: Evaluate the integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the integral.

Q66: Find the center of mass of a

Q68: Evaluate the improper integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the

Q69: Evaluate the double integral over the

Q70: Find the volume of the indicated

Q71: Evaluate the improper integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the

Q72: Solve the problem.<br>-Find the average distance from