Solved

Solve the Problem. -Write an Iterated Triple Integral in the Order for Order

Question 1

Multiple Choice

Solve the problem.
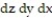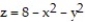-Write an iterated triple integral in the order Solve the problem. -Write an iterated triple integral in the order for the volume of the region enclosed by the paraboloids and . A) B) C) D) for the volume of the region enclosed by the paraboloids Solve the problem. -Write an iterated triple integral in the order for the volume of the region enclosed by the paraboloids and . A) B) C) D) and Solve the problem. -Write an iterated triple integral in the order for the volume of the region enclosed by the paraboloids and . A) B) C) D) .


A) Solve the problem. -Write an iterated triple integral in the order for the volume of the region enclosed by the paraboloids and . A) B) C) D)
B) Solve the problem. -Write an iterated triple integral in the order for the volume of the region enclosed by the paraboloids and . A) B) C) D)
C) Solve the problem. -Write an iterated triple integral in the order for the volume of the region enclosed by the paraboloids and . A) B) C) D)
D) Solve the problem. -Write an iterated triple integral in the order for the volume of the region enclosed by the paraboloids and 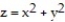. A) 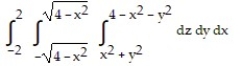B) 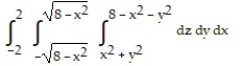C) 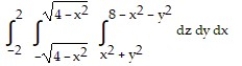D)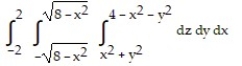

Correct Answer:

verifed

Verified

Related Questions

Q2: Express the area of the region bounded

Q3: Change the Cartesian integral to an equivalent

Q4: Use the given transformation to evaluate the

Q5: Choose the one alternative that best completes

Q6: Evaluate the improper integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the

Q7: Integrate the function f over the given

Q8: Evaluate the cylindrical coordinate integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg"

Q9: Find the volume under the surface

Q10: Find the center of mass of a

Q11: Evaluate the spherical coordinate integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate