Multiple Choice
Consider the boundary value problem 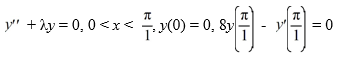
Which of the following statements are true? Select all that apply.
A) = 0 is an eigenvalue.
B) There is one negative eigenvalue 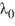 = -
= - 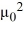 such that tanh
such that tanh 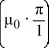 =
= 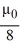 ; the corresponding eigenvectors are
; the corresponding eigenvectors are 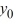 (x) = C sinh(
(x) = C sinh( 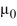 x) , where C is an arbitrary nonzero real constant.
x) , where C is an arbitrary nonzero real constant.
C) There are infinitely many positive eigenvalues 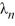 = -
= - 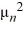 , n = 1, 2, 3, ... such that
, n = 1, 2, 3, ... such that 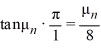 ; the corresponding eigenvectors are
; the corresponding eigenvectors are 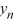 (x) =
(x) = 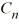 sin(
sin( 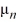 x) , where
x) , where 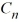 is an arbitrary nonzero real constant.
is an arbitrary nonzero real constant.
D) There are infinitely many negative eigenvalues 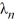 = -
= - 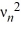 , n = 1, 2, 3, ... such that
, n = 1, 2, 3, ... such that 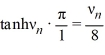 ; the corresponding eigenvectors are
; the corresponding eigenvectors are 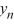 (x) =
(x) = 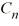 sin(
sin( 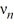 x) , where
x) , where 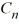 is an arbitrary nonzero real constant.
is an arbitrary nonzero real constant.
Correct Answer:

Verified
Correct Answer:
Verified
Q9: Consider the eigenfunction problem<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q10: Consider the boundary value problem<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q11: Consider the eigenfunction problem<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q12: Consider the Sturm-Liouville problem<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q13: Consider the boundary value problem<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q14: Consider the boundary value problem<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q15: Consider the boundary value problem<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q16: Consider the boundary value problem<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q17: The singular Sturm-Liouville boundary value problem
Q19: Consider the boundary value problem<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"