Multiple Choice
Consider the following periodic function with period 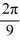 :
:
F (t) = 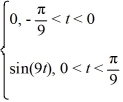
F 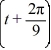 = f (t)
= f (t)
The Fourier representation has the form 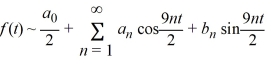
Which of these are the coefficients 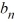 ?
?
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q21: Suppose that both ends of a string
Q22: Consider the boundary value problem <img
Q23: Consider the following periodic function with period
Q24: Consider the conduction of heat in a
Q25: Which of the following represents all
Q27: Consider the following periodic function with period
Q28: The ends of a rod 75 cm
Q29: Consider the following periodic function with period
Q30: Consider the following periodic function with period
Q31: Consider the boundary value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"