Multiple Choice
Find the Fourier series for f (x) = 4, 0 < x < 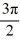
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q6: The ends of a rod 45 cm
Q7: Assume that <span class="ql-formula" data-value="\lambda"><span class="katex"><span
Q8: Suppose f (x) is defined by f
Q9: Consider the function f (x) = 7
Q10: Consider the following periodic function with
Q12: Suppose the following initial boundary value problem
Q13: Determine the function u(x, y) satisfying Laplace's
Q14: Which of the following statements are true?
Q15: Consider the following periodic function with period
Q16: Consider the following function:<br>F (x) = <img