Consider the First-Order Differential Equation - 5y = 0 $c_{n+1}-5 c_{n}=0, n=0,1,2, \ldots$

Multiple Choice

Consider the first-order differential equation 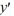- 5y = 0.
Assume a solution of this equation can be represented as a power series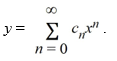
What is the recurrence relation for the coefficients C_n? Assume that C₀ is known

A) $c_{n+1}-5 c_{n}=0, n=0,1,2, \ldots$
B) $(n+1) (n+2) c_{n+1}-5 c_{n}=0, n=0,1,2, \ldots$
C) $(n+1) c_{n+1}+5 c_{n}=0, n=0,1,2, \ldots$
D) $(n+1) c_{n+1}-5 c_{n}=0, n=0,1,2, \ldots$